Quantitative Measure of Intelligence
Othman Ahmad, A.M. Alvarez & Chan Choong Wah
School of Electrical and Electronic Engineering
Nanyang Technological University, Singapore
ABSTRACT
A method of measuring intelligence quantitatively
in units of bits based on information theory is presented. The method of
measurement is simple because the proposed definition of intelligence gives
only a quantitative measure of the thinking process distinguishable from the
information processing part and knowledge. It also treats intelligence as a
resource and predicts that a C compiler uses more intelligence per instruction
than a Spice program. The term "capability for intelligence" is introduced
and shows that a human being may have a much higher capability for intelligence
than a microprocessor. The amount of intelligence measured can be used to
develop more intelligent microprocessors and algorithms, instead of using only
brute-force parallelism which requires a lot of hardware.
INTRODUCTION
Standard
text books on artificial intelligence0,0 are not known to describe a
quantitative measure of intelligence. The widely quoted test for artificial
intelligence, the Alan Turing test, is only a subjective one. It does not
allocate intelligence units to an object.
Intelligence
had been viewed with awe for a long time. There is a believe that only human
beings can have intelligence and intelligence cannot really be measured judged
from the failures of the known human intelligence tests such as IQ(intelligence
quotient) test. By breaking this mystical view of intelligence and treating it
like any scientific concept, hopefully we can make rapid advances in creating
intelligent machines.
In
discussing a controversial topic such as this measure of intelligence, it is
worthwhile for us to consider the methodologies which may be used. Among the
most successful method is the scientific method.
Quoted
from Marion & Hornyak0,
1 Scientific method is to base
conclusions on the results of observations and experiments, analyzed by logic
and reason.
2 Scientific method is not a
prescription for learning scientific truth.
3 The ultimate answer to any
question concerning natural phenomena must be the result of experimental
measurement.
4 A theory attempts to explain why
nature behaves as it does.
5 To construct a theory, we
introduce certain unexplained fundamental concepts e.g. energy, time,
space and electric charge.
6 Laws of physics tell how things
behave in terms of the theory.
7 Theories are judged based on
predictive power, comprehensiveness and simplicity.
To
be useful to an engineer, it must also allow him to minimize cost (in dollars)
in solving a problem.
Allen
Newell0 noted that
intelligence is different from knowledge and does not discount that
intelligence can be quantitatively measured. G.N. Saridis0 uses similar ideas outlined
in this paper, in measuring the intelligence of a control system as its total
entropy, by minimizing this intelligence value for maximum precision. The
quantitative measure in this paper is more general and works at lower levels
than that used by G.N. Saridis. Another view of this method, especially for students
of artificial intelligence, is presented in Appendix A.
In
line with the scientific method, we do not explain the concept of intelligence
because it is treated as one of those unexplained concepts such as
energy.
INTELLIGENCE
THEORY
Based
on our usual observation, an object that just do repetitive tasks is considered
as less intelligent. The reverse, that is an object that do not do repetitive
tasks can be considered to be more intelligent. If the tasks are done
repeatedly in the same pattern, we should be able to predict the tasks which
may be executed. Therefore we can conclude that an object that executes
predictable tasks has less intelligence and vice versa, that is, an intelligent
object is capable of autonomous operations and the operations are executed in
an unpredictable manner.
The
operations are identified by assigning a unique symbol to each one of them. We
must first consider the case when we do not have access to the way the
operations are generated and the amount of time that we observe the operations
are limited(sampling time).
If
we just consider the symbols and the occurrence of these symbols as events then
information theory can be applied.
The
amount of information is proportional to the degree of unpredictability. An
event that is sure to happen has zero information.
Definition (1):
The
information I(xi) of an event X=xi with probability P(xi)
is
MEANING
EXTRACTION PROCESS
OBJECT (Symbol) 6
MEANING (Symbol)
Compiler
Terms
lexical analysis
9
syntax
analysis
9
semantic
analysis
Operations
on symbols
convert text
to unique objects by giving unique symbols
find
relationship between objects and assigning unique symbols to each
relationship
convert relationship
symbols to predefined actions
Figure
1
|
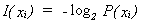 (1) (1)
|
Equation
1 is known as the
logarithmic measure of information as proposed by C. E. Shannon. P(xi)
is not the self-information as described by Proakis0, it's relationship to previous occurrences of xi
is not stated so it can depend on any of them in various degrees.
This
implies that a perfect truth table (or any highly parallel network structures
such as Neural Networks), which gives a definite output for a fixed input
pattern, has zero information generating value. They do not use intelligence
for their functions. They must have enough predictive hardware to store all
possible combinations of input and output patterns. Our intuition tells us that
this predictive hardware is what we usually call knowledge. Although knowledge
is not defined in an information theoretic way here, it gives a possible direction
for future research work.
Definition (2):
In
order to have autonomous operation, a machine must have memory to store
instructions. The number of instructions in such machine is its program size,
Z.
An
autonomous machine which executes instructions in a predictable manner
(instructions such as unconditional branches) has zero intelligence because the
information content of all possible events (execution of instructions) is zero.
Definition (3):
A
unit instruction at time t, at, is
an indivisible event in time, and can be stored in one unit of memory (the unit
of the memory must be sufficient to store all possible instruction sizes). The
number of unit-instructions which can be stored is Z.
Definition (4):
The
intelligence content, Q, of a sequence of instructions from time t=0 to T, is
the total information content of that occurrence of instructions, I(at).
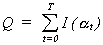 (2) (2)
|
Equation 2 represents the joint probability of events as the
product of the probability of each event.
Definitions
1-4 imply that each instruction has equal importance. Therefore an instruction
that executes a complex pattern matching in one cycle has the same weight as an
instruction that does nothing (NOP). This result comes from equation 1. A program (a sequence of
instructions) may have a large intelligence content but zero information
processing ability.
Please
note that we are only measuring the intelligence content of a machine, not its
throughput. A stupid machine can be very productive indeed. The semantic
content of an instruction can also be represented by a symbol so this model
assumes that syntax is identical to semantics. Jumarie0 attempted to relate symbols and meanings but it
introduces more complexity. It should be apparent that the meaning of a symbol
is determined by consensus, e.g. a pen is red because we all agree that it is
red, not by reason(1).
The different languages describing "red" are just redundancies.
IMPLICATIONS
Intelligence
can be thought of as a resource which should be used at the correct
circumstances, similar to energy and time. There must be a time, space and
intelligence relationship whereby we can increase intelligence only to increase
the time of processing (number of sequential instructions) but decreasing the
space requirement (less hardware). For the same information processing rate,
increasing parallelism in the program (by utilising more hardware) results in the
reduction in the number of sequential instructions (implying a reduction in
intelligence). Of course we can design circumstances whereby we optimise all
these relationships where we can get
the maximum intelligence while reducing time by maximising the number of
random conditional branches.
An
analogy is a student trying to take his examination. He has 2 options open to
him. One is to remember as much as possible so that he can just regurgitate
facts with little intelligence. The other is to concentrate on deductive
reasoning by remembering only key concepts from which he can recover
information or even invent alternative solutions. The second method can be
called the more intelligent method whereas the first one is more of a reflex
action. The throughput is the number of correct answers, which may be the same
for both cases.
A
stupid machine may look intelligent if it is controlled by pseudo-random
sequence generators which is common in Spread Spectrum systems. However
pseudo-random is actually predictable. The degree of randomness (or the
inverse, predictability), is dependent on the period of the sequences. The
pattern of the sequences can only be detected if we are able to sample twice
the period of one complete cycle of sequences. The information content
measurable is dependent on the sampling period that the observer can make.
If
we have full access to the algorithm of the code generation, we would discover
that the intelligence of the pseudo-random pattern generator is virtually zero.
If
the observer has no access, he must try to obtain as many samples as he can.
The information content that he has measured of the pseudo-random generator is
his perceived intelligence of the pseudo-random generator, which must be wrong
if the observer has not broken the code generation algorithm. Definitions 1-4
does not fail to quantify the intelligence of the pseudo-random generator, it
is just that the sampling time is not sufficient.
MICROPROCESSOR
EXAMPLE
The
development of this measure of intelligence is due to efforts in analyzing the
critical information flow in microprocessors(2).
Let us apply these definitions to a typical general purpose program running on
a typical microprocessor.
A
program counter generates the pattern which identify the instructions which may
be executed. The sampling period is the time that the value of the program
counter changes.
The
only instructions which may have intelligence are the conditional branches.
Some conditional branches such as those used in loops are very predictable.
Although we have defined intelligence, the
actual amount of information is very hard to determine. We have to
resort to statistical sampling techniques and make some assumptions which will
reduce the accuracy of our measurement.
Let
us assume that only and all conditional branches are truly random, there are bS of them, where S is the number of instructions
which have been executed and each branch may choose B # Z equally likely addresses. For a
DLX0 microprocessor B=2. For
man, B is very large. B determines the capacity for intelligence. For the same
microprocessor DLX, b are 0.20 and 0.05 for Free Software Foundation's
GNU C Compiler and Spice respectively.
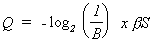 3 3
|
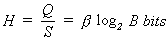 (3) (3)
|
H in equation 3 is
the average intelligence(entropy) of each instruction measured at each
instruction execution. For simple problems (requiring less B), the rate of
intelligence of a machine is higher than man.
We
can conclude that a C compiler program
uses more intelligence per step(b) than Spice which is mainly a numerical program,
and total intelligence depends only on b, B and S.
If
a microprocessor is to be designed for highly intelligent programs, such as
expert systems, it must be optimised for minimal pipeline flushes on
conditional jumps and each conditional branch may choose many instructions. We
now have a concrete guideline in designing microprocessors.
USES
OF INTELLIGENCE DEFINITIONS
This
measure should reinforce our intuition about our intelligence versus reflex
action. Pattern recognition is just a reflex action after a period of training.
Initially a lot of intelligence is required to incorporate knowledge into our
memory. After the initial training period, we require less intelligence.
Parallel brute force hardware is not the ultimate solution. They still need
intelligent pre and post processors which is more likely to be sequential.
Although
a human being has a lot of organs that exploit parallelism, our consciousness
is sequential. It seems as though there is a master computer which is
sequential (Von Neumann Machine) which controls other distributed processors of
various degrees of intelligence. This argues the case for SIMD supercomputers
which may have slave MIMD machines.
CONCLUSION
Four
definitions are proposed to be used for
measuring intelligence quantitatively in units of bits based on information
theory. This intelligence theory is used to

Figure
2: Information Theoretical Analysis
of a Processor: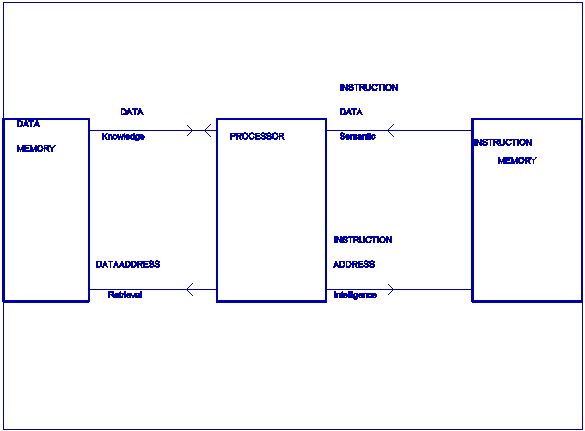
|
support some microprocessor design decisions and
verified using data for C compiler and Spice programs. The results match with
our normal intuition that a C compiler uses more intelligence than Spice. The
definitions of intelligence for quantitative measure is simplified through
deliberate and careful study by separating intelligence from knowledge and
information processing. Hopefully its predictive power can be verified further
through more exhaustive study of programs that can be thought of as intelligent,
such as expert systems, in line with the objectives of the scientific method.
However care must be taken in using these knowledge based systems because they
can be deterministic in their operations. It is not surprising because
knowledge and intelligence are interchangeable provided there is sufficient
hardware to do the prediction through its knowledge database. In addition, the
importance of sampling period is shown and the term "capability for
intelligence" introduced to explain the fact that a human being is capable
of great intelligence compared to existing computers.
ACKNOWLEDGEMENTS
The
authors wish to acknowledge the contributions of the staff of the Nanyang
Technological University, especially P. Saratchandran, who gave critical
analysis of the initial ideas and therefore helps to improve the presentation
of this paper. However the principal author accepts responsibility for any
remaining weaknesses and errors.
REFERENCES
[1] M. W. SHIELDS
'An Introduction to Automata Theory' Blackwell Scientific Publications
(1987)
[2] G. F. LUGER, W. A. STUBBLEFIELD 'Artificial
Intelligence and the Design of Expert Systems' The Benjamin/Cummings
Publishing Company, Inc. (1989)
[3] J.B MARION & W.F. HORNYAK 'Principles
of Physics' Saunders College Publishing (1984)
[4] A. NEWELL 'Unified Theories of
Cognition' Harvard University Press (1990)
[5] G.N. SARIDIS 'An Integrated
Theory of Intelligent Machines by Expressing the Control performance as Entropy'
Control-Theory and Advanced Technology, Vol 1,No.2,pp.125-138,August 1985,Mita
Press
[6] J.G. PROAKIS 'Digital
Communications' 2nd Edition, McGraw-Hill Book Company (1989)
[7] G. JUMARIE 'Relative
Information:Theories and Applications' Springer-Verlag Berlin Heidelberg
(1990)
[8] J. L. HENNESSY, D. A. PATTERSON 'Computer
Architecture A Quantitative Approach' Morgan Kaufmann Publishers, Inc.
(1990)
APPENDIX
A
Lewis
Johnson, editor of SigArt, interprets Allen Newell's definition of Intelligence
as "the ability of an agent to act in an uncertain environment in order to
achieve its goals".
Can't
we quantify the "ability of the agent" by measuring the
"uncertainty of the environment" in order to achieve just one
particular goal or set of goals?
We
can measure the uncertainty using information theory. The beauty of using information theory as a definition is that it
is exact. However, to measure it would incur measurement error. We must resort
to statistical techniques to minimize the error.
An
agent wants to achieve a goal in an uncertain environment. In order to achieve
it he must do something. He must have alternatives. Otherwise it would be
impossible for him to achieve the goal. If he cannot even generate the alternatives
then he must be stupid. No point in measuring his intelligence.
The
number of alternatives which are required to solve a goal in an uncertain
environment would indicate the uncertainty of the environment. The more
alternatives, the more uncertain the environment. The goal is just one of the
alternatives. The uncertainty is just by "definition" to be log2
of the number of alternatives. Let us say this is INTL bits of uncertainty.
This
definition is the information theory
stated in a different way to make it clearer to students of AI. Why should we
use log2?
If
the agent can generate all alternatives in just one step, then we may say that
he has generated INTL bits of intelligence, because he has managed to reach his
goal in an environment with INTL bits of uncertainty.
The
above paragraph is just a standard measurement theory. For example, the horse
power is defined by the rate that a particular horse can drag a particular
weight. If an engine can drag the same weight at the same rate, then that engine has one horse power.
He
may just generate 2 alternatives at one step. He would therefore need many
steps to come to the goal. If there is no loss in generating alternatives, he
would need INTL steps.
For
example: let INTL =3 so there are 23=8 alternatives. At each step he
can eliminate half of the alternatives because the solutions must be possible.
The alternatives are stored in his knowledge data base. If he can't eliminate
half of the alternatives, then there is loss. We are making an assumption that
there is no loss. This loss reflects how efficient the decision tree is built
up. So he must take 3 steps to reach his goal. On the other hand the decision
tree may not be balanced, leading to other deviations.
Log22
is 1. Therefore he can generate intelligence of 1 bit per step. His capability
for intelligence is 1 bit per step.
For
each step he uses his intelligence resource. When he reaches his goal, he has
used up 3 intelligence bits, which is the same as the uncertainty of the
environment.
The
amount of intelligence required is 3 bits, the uncertainty of the environment.
The amount of intelligence used by the agent is 3 bits because there is no
loss. Because we are using logarithmic
scale, we can just add all them up. If we use number of alternatives as units,
then we must use division or multiplication.
Please
note that the definitions for quantitative measure of intelligence which is
presented is not just unpredictability. In fact it is the ability to generate
unpredictable sequences of instructions.
My
discussions above assume that we have full access to the knowledge data base and the agent's ability
to test alternatives.
What
happens if we just observe from outside? If the environment for the goal were
very uncertain, then we would observe that the agents generate various
alternatives which the observer cannot be certain of.
If
the observer can only have access to one time slice equivalent to the time
slice that the agent generates one alternative, then we would have to add the
intelligence units measured at each step to come up with a method to measure
the total intelligence units consumed by the agent in coming to that goal. What
happens if we are capable of observing all 3 steps and get enough samples to
decode the goal for each input. We simulate the goal by just using look‑up
table. For each input there must be a goal. The size of this lookup table(in
bits) depends on the uncertainty of the environment.
So
there are 2 methods of achieving the same goal:
1)Generating alternatives for each input step by
step which takes longer or
2)Using lookup table which is faster but needs
more storage bits.
We
can generalize that 1 is using intelligence, 2 is using knowledge.
Expert
systems are just interpreters or compilers. The rules are the grammar. The
objects are the tokens. A C compiler can be viewed as an expert system with C
language syntax as its knowledge database.
If
it is not intelligence, what actually it is that we are measuring? What is the
relationship between knowledge and this quantity? How do we define the
quantitative measure of knowledge?
